15. Мышка и зернышки

В индийском храме пол прямоугольной формы выложен одинаковыми квадратными плитками 1 × 1, на каждую из которых высыпано от 0 до k (k ≤ 30000) зернышек. Размеры пола m × n. Мышка выбегает из левого нижнего угла пола храма и двигается к входу в другую норку, расположенную в противоположном углу. Мышка может двигаться только вправо или вперед, собирая все зернышки с плитки, на которой она находится.

Найти маршрут, двигаясь по которому мышка соберет наибольшее количество зернышек.

Вход. Первая строка содержит числа m и n (1 ≤ m, n ≤ 100) – размеры пола. Далее идут m строк, начиная сверху, в каждой из которых размещено чисел – количество зернышек на соответствующей плитке.

Выход. Вывести маршрут движения мышки в формате: RRFFFRF (F – шаг вперед, R – шаг вправо).

Пример входа	Пример выхода
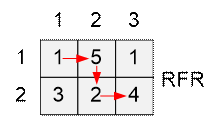
2 3 3 2 4 1 5 1	RFR

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Для удобства дальнейших вычислений перевернем доску снизу вверх. Клетки по вертикали и по горизонтали будем нумеровать с 1. Тогда маршрут мышки будет пролегать с левого верхнего угла – клетки с координатами (1, 1), в правый нижний – клетку с координатами (m, n). А движение вниз по доске будет кодироваться буквой F.

Пусть на плитке с координатами (i, j) находится a[i][j] зернышек. Пусть res[i][j] содержит максимальное количество зернышек, которое можно собрать при движении из левого верхнего угла в клетку (i, j). Поскольку на плитку (i, j) можно попасть или из плитки (i – 1, j), или из (i, j – 1), то

res[i][j] = max(res[i – 1][j], res[i][j – 1]) + a[i][j]

Можно также обойтись и без массива res, совершая вычисления в самом массиве а. Будем проходить плитки пола (ячейки массива) сверху вниз и слева направо, положив

а[i][j] = max(a[i – 1][j], a[i][j – 1]) + a[i][j]

Изначально все ячейки нулевой строки и нулевого столбца массива а инициализируем -1. Однако для корректного пересчета значения а[1][1] следует обнулить одну из ячеек: a[0][1] или a[1][0]. В таком случае новое значение ячейки а[1][1] станет равным max(a[0][1], a[1][0]) + a[1][1] = 0 + a[1][1] = a[1][1]. В дальнейшем все значения а[i][j] будут пересчитаны корректно.

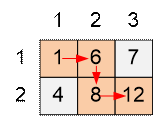
После проведенных вычислений a[i][j] уже будет содержать максимальное количество зернышек, которое можно собрать по достижении плитки (i, j). Состояние массива а по окончанию вычислений:

Реализация алгоритма

Входную информацию о зернышках будем хранить в массиве a. То есть на плитке с координатами (i, j) находится a[i][j] зернышек. Маршрут движения мышки будем сохранять в массиве pos, имеющему длину m + n – 1 (m и n – размеры пола).

#define MAX 102

int a[MAX][MAX];

char pos[2*MAX];

Считываем входные данные. Поскольку на плитках может находиться и 0 зернышек, то инициализируем ячейки массива числами -1. Доску переворачиваем снизу вверх.

scanf("%d %d",&m,&n);

memset(a,-1,sizeof(a));

for(i = 1; i <= m; i++)

for(j = 1; j <= n; j++)

scanf("%d",&a[m-i+1][j]);

Пересчитаем ячейки массива а так, чтобы а[i][j] содержало максимальное количество зернышек, которое можно собрать по достижении плитки (i, j).

a[0][1] = 0;

for(i = 1; i <= m; i++)

for(j = 1; j <= n; j++)

a[i][j] = max(a[i-1][j],a[i][j-1]) + a[i][j];

Начиная с плитки (i, j) = (m, n), двигаемся до плитки (1, 1) записывая маршрут движения мышки в массиве pos. Из плитки (i, j) необходимо двигаться в (i – 1, j) или (i, j – 1), в зависимости от того, какое из значений a[i – 1][j] или a[i][j – 1] больше.

i = m; j = n; ptr = 0;

while(i + j > 2)

{

if (a[i-1][j] > a[i][j-1])

{

pos[ptr] = 'F';

i--;

}

else

{

pos[ptr] = 'R';

j--;

}

ptr++;

}

Выводим маршрут движения мышки.

while(ptr--) printf("%c",pos[ptr]);

printf("\n");